上面,我们对RNA表达数据进行了差异分析,下面,我们将进行主成份分析(PCA),用于对数据进行区分和归类。
1 | > pcaData <- data[rownames(result_select),] # 这里,首先使用差异表达数据,即筛选出来的4913个基因在611个样本中的表达水平 |
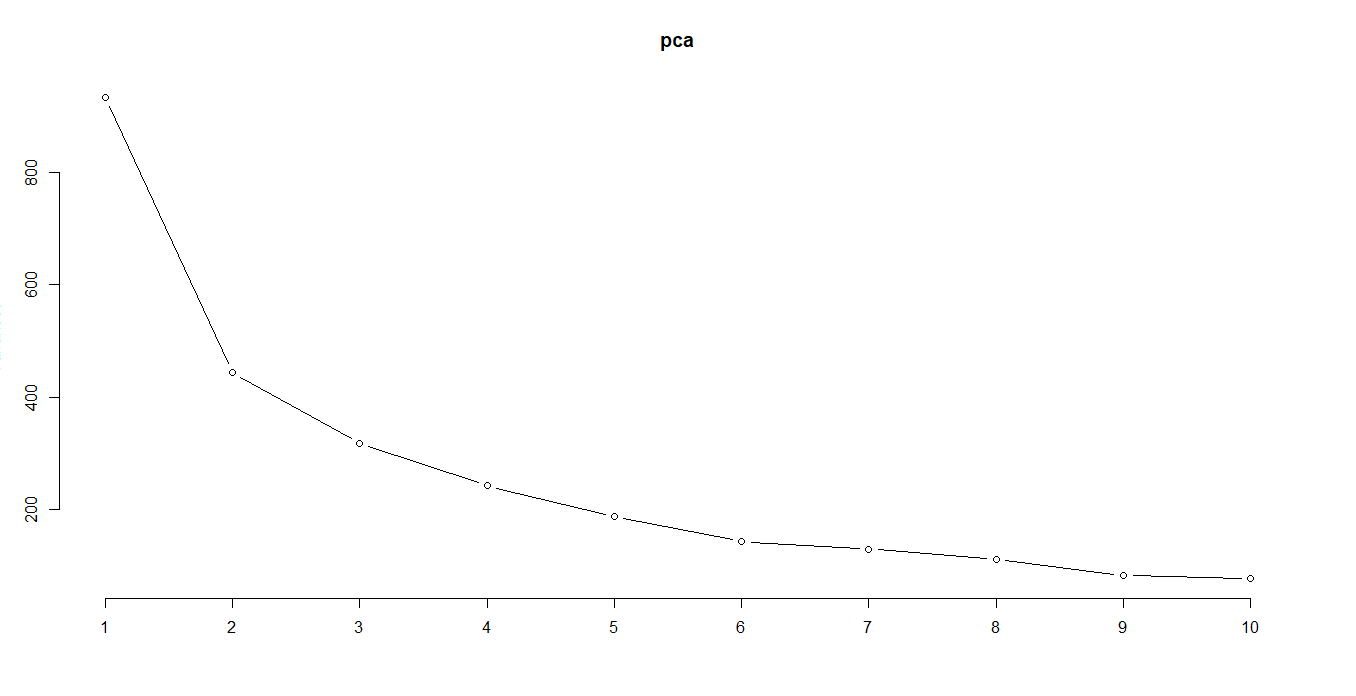
1 | > str(pca) # 看一下数据结构 |
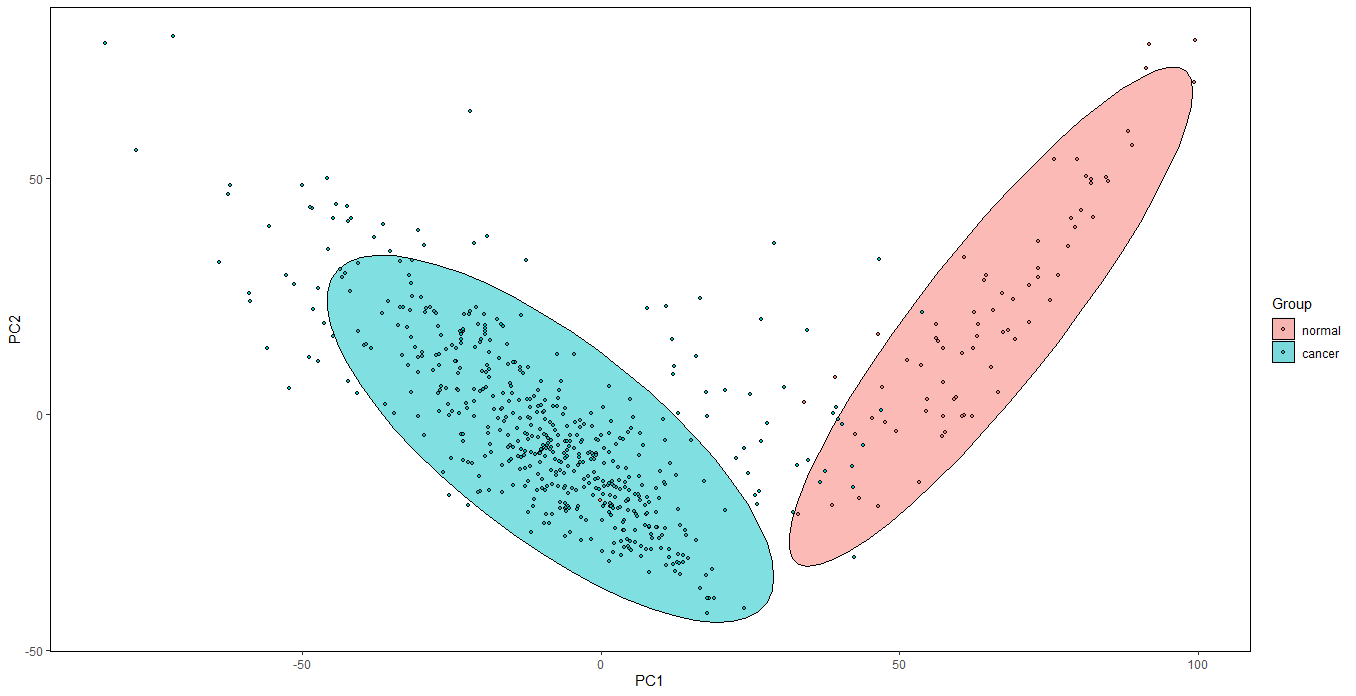
如图,肿瘤样本与正常样本被很好地分为两组,可以明确区分,这也可被用于预测一个未知样本是否是肿瘤样本或是正常样本。
上面,我们对RNA表达数据进行了差异分析,下面,我们将进行主成份分析(PCA),用于对数据进行区分和归类。
1 | > pcaData <- data[rownames(result_select),] # 这里,首先使用差异表达数据,即筛选出来的4913个基因在611个样本中的表达水平 |

1 | > str(pca) # 看一下数据结构 |

如图,肿瘤样本与正常样本被很好地分为两组,可以明确区分,这也可被用于预测一个未知样本是否是肿瘤样本或是正常样本。

WeChat Pay