在R中使用dnorm()作正态分布曲线

发表于 | 分类于 | | 热度 °C

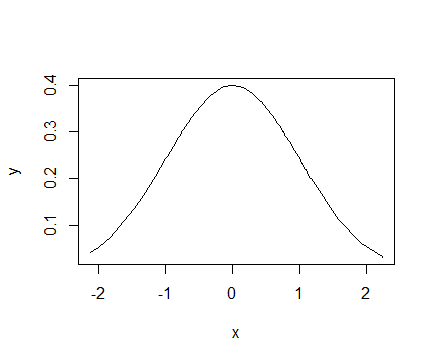
在R中，dnorm()是正态分布的概率密度函数，d代表density，norm代表正态分布，返回给定x在标准正态分布下的概率密度。

对于一个给定的正态分布，X ∼ N(μ,σ2)，μ代表均值，σ2代表方差，dnorm()可以计算给定x下的概率密度，即P(X<=x|μ=a,σ=b)，比如，对于标准正态分布 X ∼ N(0,1)，要计算x=1时的概率密度，即dnorm(1)=P(X<=1|μ=0,σ=1)

1
2
3
4
> dnorm(1) # 默认为标准正态分布，故亦可以写作下面这种形式
[1] 0.2419707
> dnorm(1,mean=0,sd=1)
[1] 0.2419707

根据dnorm()的性质，我们可以利用dnorm()来绘制正态分布曲线。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
> x <- rnorm(100)
> x
  [1]  0.067624027  0.446922747 -0.779610273  1.019910795 -0.611558691 -0.042208614  1.057542821
  [8]  0.168769225  0.292759062  0.069769967 -1.884478653  0.210965341  0.487999663  0.079415785
 [15]  0.547819110  1.218320307 -0.829277733 -0.180677502 -0.722302587 -0.275027962  1.147344053
 [22]  0.057776822  0.620030502 -0.006237543  0.150433226  1.259527763 -0.828779833 -1.581627780
 [29] -0.291715425 -0.275497338 -0.531884989 -0.022351625 -0.213368332 -0.661274484  1.052272355
 [36] -1.491285952 -0.490500385 -0.289660378 -1.223280167 -0.407513962 -0.951917561  0.880820238
 [43]  0.193889773 -1.401977549 -0.571268441 -0.680519505 -0.593670209  1.149960529 -0.366887812
 [50] -1.401057013  0.520541718 -1.871404951 -1.529649961  0.380110232 -0.646800728 -1.745816661
 [57] -1.658797701 -0.809181810 -1.228480576 -0.228532084  1.529535839  0.064914455  0.243817469
 [64]  0.623980927 -1.621383762 -1.790768314  0.816892971 -0.278317894 -0.090169109  0.350612752
 [71]  2.134799802 -0.105936765 -0.606534781 -1.037662539 -0.956454603 -1.271927292 -0.787623941
 [78] -0.001952851 -0.906800210  2.335462375 -0.778546226  0.520102904 -1.076871213  2.310164950
 [85]  0.001740659 -0.808784690  0.750435109 -0.453002059  2.304120907  0.192156923  0.659194960
 [92] -0.807322096 -0.976952123 -0.392610629 -1.173103468  2.769663266 -0.085446868  2.340928468
 [99]  0.309876876 -1.262045807
> x <- x[order(x)]
> x
  [1] -1.884478653 -1.871404951 -1.790768314 -1.745816661 -1.658797701 -1.621383762 -1.581627780
  [8] -1.529649961 -1.491285952 -1.401977549 -1.401057013 -1.271927292 -1.262045807 -1.228480576
 [15] -1.223280167 -1.173103468 -1.076871213 -1.037662539 -0.976952123 -0.956454603 -0.951917561
 [22] -0.906800210 -0.829277733 -0.828779833 -0.809181810 -0.808784690 -0.807322096 -0.787623941
 [29] -0.779610273 -0.778546226 -0.722302587 -0.680519505 -0.661274484 -0.646800728 -0.611558691
 [36] -0.606534781 -0.593670209 -0.571268441 -0.531884989 -0.490500385 -0.453002059 -0.407513962
 [43] -0.392610629 -0.366887812 -0.291715425 -0.289660378 -0.278317894 -0.275497338 -0.275027962
 [50] -0.228532084 -0.213368332 -0.180677502 -0.105936765 -0.090169109 -0.085446868 -0.042208614
 [57] -0.022351625 -0.006237543 -0.001952851  0.001740659  0.057776822  0.064914455  0.067624027
 [64]  0.069769967  0.079415785  0.150433226  0.168769225  0.192156923  0.193889773  0.210965341
 [71]  0.243817469  0.292759062  0.309876876  0.350612752  0.380110232  0.446922747  0.487999663
 [78]  0.520102904  0.520541718  0.547819110  0.620030502  0.623980927  0.659194960  0.750435109
 [85]  0.816892971  0.880820238  1.019910795  1.052272355  1.057542821  1.147344053  1.149960529
 [92]  1.218320307  1.259527763  1.529535839  2.134799802  2.304120907  2.310164950  2.335462375
 [99]  2.340928468  2.769663266
> y <- dnorm(x)
> y
  [1] 0.06757154 0.06925106 0.08026962 0.08691050 0.10078725 0.10716547 0.11421053 0.12382908 0.13121666
 [10] 0.14931322 0.14950598 0.17766810 0.17990644 0.18758545 0.18878514 0.20048328 0.22340604 0.23286176
 [19] 0.24754664 0.25250071 0.25359620 0.26445562 0.28286393 0.28298071 0.28755931 0.28765171 0.28799187
 [28] 0.29255158 0.29439449 0.29463863 0.30734049 0.31648104 0.32059376 0.32364303 0.33089951 0.33191354
 [37] 0.33448585 0.33887894 0.34632094 0.35372559 0.36003862 0.36715457 0.36935018 0.37297575 0.38232376
 [46] 0.38255222 0.38378647 0.38408633 0.38413596 0.38865936 0.38996373 0.39248353 0.39670996 0.39732378
 [55] 0.39748856 0.39858707 0.39884264 0.39893452 0.39894152 0.39894168 0.39827697 0.39810262 0.39803114
 [64] 0.39797247 0.39768622 0.39445366 0.39330100 0.39164452 0.39151355 0.39016259 0.38725882 0.38220718
 [73] 0.38024086 0.37515981 0.37113833 0.36102484 0.35415863 0.34847386 0.34839431 0.34335464 0.32917774
 [82] 0.32836988 0.32103423 0.30103915 0.28576211 0.27066844 0.23715353 0.22933371 0.22806219 0.20656550
 [91] 0.20594562 0.18993171 0.18047850 0.12385070 0.04085919 0.02805958 0.02767102 0.02609189 0.02576054
[100] 0.00861323

plot(x,y,type="l")

  • 本文作者：括囊无誉
  • 本文链接： R/R_dnorm/
  • 版权声明： 本博客所有文章均为原创作品，转载请注明出处！
------ 本文结束 ------
坚持原创文章分享，您的支持将鼓励我继续创作！